Эйнштейн теңдеулерінің алатын орны

Нуркасымова Сауле Нуркасымовна
Л.Н. Гумилев атындағы Еуразия ұлттық университеті
педагогика ғылымының докторы, профессор

Диярат Дина
Л.Н. Гумилев атындағы Еуразия ұлттық университеті
магистрант

Анотация: Бұл мақалада  А. Эйнштейннің жалпы салыстырмалылық теориясы және Эйнштейн теңдеулері қарастырылады. Эйнштейннің теория кеңістік пен уақытты статикалық фон ретінде емес, материя және энергия әсеріне жауап беретін динамикалық геометриялық объект ретінде сипаттайды. Эйнштейн теңдеулері гравитацияны класcикалық Ньютон тартылыс заңы сияқты күш емес, кеңістік-уақыт қисықтығы ретінде көрсетеді.

Сонымен қатар Ғаламның ірі масштабтағы құрылымын түсіндіруде, жұлдыздар эволюциясында, қарақұрылықтардың табиғатын анықтауда және космологияда Эйнштейн теңдеулері негізгі математикалық аппарат ретінде қолданылады.

Бұл мақалада Эйнштейн теңдеулерінің құрылымы, оның тензорлық табиғаты, космологиялық тұрақтының рөлі және электромагниттік өріс қосылған жағдайдағы шешімдер қарастырылады.

Түйін сөздер: Жалпы салыстырмалылық, Эйнштейн теңдеулері, метрика тензоры, Риччи тензоры, скалярлық қисықтық, космологиялық тұрақты, энергия–импульс тензоры, электромагниттік өріс, Фридман моделі, Реисснер–Нордстрём–де Ситтер шешімі, ғаламның кеңеюі, гравитациялық өріс, кеңістік-уақыт геометриясы.

Кіріспе

Қазақстан Республикасының Президенті Қасым-Жомарт Тоқаев өзінің жастар мен ғылым туралы жолдауларында ғылымның іргелі бағыттарының дамуы елдің интеллектуалдық әлеуеті үшін шешуші маңызға ие екенін бірнеше рет атап өткен еді. Президенттің: «Ғылымсыз елдің болашағы бұлыңғыр. Біз жаңа технология мен іргелі зерттеулерге сүйенген мықты ғылыми мектеп қалыптастыруымыз керек» деген сөзі қазіргі физикадағы жалпы салыстырмалылық теориясы сияқты  ілімдердің маңызын ерекше етіп көрсетеді [1].

Қазіргі заманғы физика ғылымында гравитация табиғатын терең түсіндіру және ғаламның жалпы құрылымын сипаттау мәселелері ерекше орын алады. Осы тұрғыдан алғанда Альберт Эйнштейннің жалпы салыстырмалылық теориясы (ЖСТ) ХХ ғасырдың ең ірі ғылыми төңкерістерінің бірі болып табылады. Бұл теория кеңістік пен уақытты абсолют, өзгермейтін фон ретінде қарастырмай, керісінше материя мен энергияның әсеріне жауап беретін динамикалық геометриялық орта ретінде сипаттайды. Эйнштейн өріс теңдеулері гравитацияны күш деп түсіндірмей, кеңістік-уақыттың қисықтығы арқылы бейнелейді. [1]

Эйнштейн теңдеулері тек гравитациялық өзара әрекеттесуді сипаттау ғана емес, сонымен бірге ғаламның кеңеюін, оның геометриялық қасиеттерін, жұлдыздар мен қарақұрылықтардың эволюциясын және жоғары энергиялы өрістердің динамикасы түсіндірудің негізгі математикалық құралы болып табылады. Космологиядағы Фридман модельдері, қарақұрылықтардың Реисснер–Нордстрём–де Ситтер шешімдері, гравитациялық толқындар теориясы — барлығы да осы теңдеулерден шығады. [2]

Қарастырып отырған тақырыпта  Эйнштейн теңдеулерінің математикалық құрылымы, олардың тензорлық табиғаты, космологиялық тұрақтының рөлі, энергия–импульс тензорының физикалық мағынасы және электромагниттік өрісі бар кеңістік-уақыт үшін кешенді түрде қарастырылады. Сондай-ақ ғаламның кеңеюін сипаттайтын масштаб факторы және Фридман теңдеулері арқылы космологиялық модельдердің физикалық интерпретациясы талданады.[3]

Эйнштейн теңдеулерінің жалпы түрін қарастырамыз.

Жалпы салыстырмалылық теориясында негізгі динамикалық айнымалы — метрика тензоры g_μν . Ол кеңістік-уақыттың барлық геометриялық қасиеттерін анықтайды. Эйнштейн теңдеулері:

Gμν + Λgμν = 8πTμν

Мұндағы Gμν — Эйнштейн тензоры,
Λ — космологиялық тұрақты»
Tμν — энергия-импульс тензоры

Космологиялық тұрақты Λ мүшесі ғаламның динамикасына жауап береді.
Егер:

Λ>0-ғалам үдейді
Λ<0-ғалам жинақталуы мүмкін
Λ=0-классикалық ЖСТ

Қазіргі космологияда Λ қараңғы энергиямен байланысты. [4]

Ғаламдағы материя біркелкі бөлінбеген: галактикалар, жұлдыздық жүйелер, космологиялық жіптәрізді құрылымдар мен қуыстар  түзілген. Бұл құрылымдардың пайда болуы бастапқы тығыздық флуктуацияларының эволюциясының нәтижесі болып табылады. ЖСТ (Жалпы салыстырмалылық теориясы) бойынша бұл эволюция космологиялық уақыт ішінде гравитациялық тартылыстың әсерінен жүреді. Осы себепті
LSS-тің статистикалық қасиеттері:
— материя қуат спектрі P(k);
— екі-нүктелік корреляциялық функция ξ(r)ξ(r)ξ(r)
— әлсіз гравитациялық линзалау ;
— қызыл ығысу бойынша бұрмаланулар (RSD);
— биспектр және жоғары ретті статистикалар ;
— гравитациялық теорияларды тексеру үшін негізгі құрал болып саналады.
«Электромагниттік өріс тензоры » T_μν/EM деп қарастыратын болсақ, онда зарядталған денелерді сипаттайтын тензор Максвелл теңдеулері шығады:

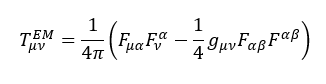
Бұл теңдеуде F_μν — электромагниттік өріс тензоры. Сфералық-симметриялы статикалық зарядталған қара саңылау жағдайында, электр өрісінің жалғыз компоненті F_tr
болады, яғни: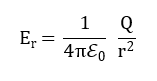

Мұндағы E_r — радиалдық электр өрісінің компоненті, Q — қара саңылаудың электр заряды ,
r — радиалдық координата, r² — вакуумның диэлектрлік тұрақтысы, осы қатынасты береді.[5]
Райсснер-Нордстрём-де Ситтер (RN-dS) Метрикасы Эйнштейн-Максвелл теңдеулерінің статикалық, сфералық-симметриялы шешімі, яғни Q заряды және Λ тұрақтысы бар қара саңылау:

ds² = f(r)dt² — f(r)^-1 dr² -r² (dθ² +sin²⁡ θ dϕ²)

Мұндағы f(r) – метрикалық функция (немесе қисықтық функциясы), ол кеңістік-уақыттың барлық қасиеттерін қамтиды, егер G=1 деп алатын болсақ, онда:

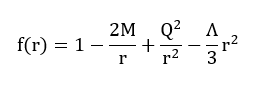
Бұл теңдеуде «M» – қара саңылаудың массасы, Q – қара тесіктің электр заряды, ал
Λ – космологиялық тұрақты болғанда Λ >0 де Ситтер кеңістігін білдіреді.
Ғаламдық құрылымның негізі – каузальдық көкжиектер (horizon), олар f(r)=0
теңдеуінің түбірлері арқылы анықталады:

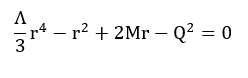
Теңдеудегі r – радиалды координата, қара саңылаудың көкжиектерінің радиусын анықтайтын айнымалы, M – қара саңылаудың массасы, кеңістік-уақыттың гравитациялық қасиеттеріне әсер ететін шама, Q – қара саңылаудың электр заряды, зарядтың кеңістік-уақыт геометриясына қосатын үлесін сипаттайды, Λ – космологиялық тұрақты, вакуум энергиясының әсерін және ғаламның кеңеюін көрсетеді.
Ғаламдық құрылымды зерттеу:
Ғаламдық құрылымды зерттеу барысында Пенроуз-Картер диаграммасын аламыз. Сонда RN-dS метрикасының каузальдық байланыстарын – яғни, жарық конустарының кеңістік-уақыттың әр нүктесінде қалай бағытталғанын – көрсететін әдісті қолданамыз. Бұл үшін Пенроуз-Картер диаграммасы таптырмас құрал болып табылады, өйткені ол шексіз кеңістік-уақытты шектеулі, ықшамдаған диаграммаға түрлендіреді.[6]
Пенроуз-Картер диаграммасы конформды түрлендіру арқылы кеңістік-уақыттың барлық аймақтарын (тіпті шексіздіктегі нүктелерді де) тіктөртбұрышқа сыйғызуға болады. Қарастыратын диаграммада:[7]
— S² кез келген нүкте екі өлшемді сфераны білдіреді,
— жарық сәулелері (нульдік геодезиялықтар) 45∘ бұрышпен жүргенін көрсетеді,
— уақытқа ұқсас жолдар тік, ал кеңістікке ұқсас жолдар көлденең болады.
Егер каузальдық қасиеттерге Λ әсерін, космологиялық тұрақты Λ (немесе қара энергия) RN-dS қара саңылауының ғаламдық құрылымын түбегейлі өзгертеді:
Шексіздіктің жойылуын Λ>0 болғандықтан, кеңістік-уақыт асимптотикалық түрде Минковский кеңістігіне емес, де Ситтер кеңістігіне ұқсайтындай алынады. Бұл бақылаушыларға қолжетімді аймақты r 2) Аймақтардың қайталануын, RN-dS шешімінде, r_-,r_+ көкжиектері арқылы өту мүмкіндігіне байланысты, диаграмманың үстіңгі және астыңғы жақтарында қайталанатын аймақтар (басқа «әлемдер») пайда болуы мүмкін.
3)Сингулярлықтың табиғаты: r=0 сингулярлығы r0 болса, онда Космологиялық Көкжиектің (r_c) пайда болуы бақыланатын аймақты шектеп, қара саңылаудың алыс аймақтағы құрылымын толығымен өзгертеді.
Эйнштейн теңдеулерінің физикалық мәні – материя кеңістік-уақытқа оның қалай ауысуын қарастырады, ал ауысу жағдайы кеңістік-уақыт материяға оның қалай қозғалу керектігін қарастырады.[10]
Эйнштейн өріс теңдеулерінің шешімдері (g_μν) ғарыштағы әртүрлі құбылыстарды сипаттайды. Шварцшильд шешімі сфералық симметриялы, айналмайтын және электр заряды жоқ массаның айналасындағы гравитациялық өрісті сипаттайды деп қарастырады. Бұл шешім қара құрдымның математикалық негізін құрады.
Керр Шешімі, айналатын қара құрдымдарды сипаттайды. Ал Фридман-Леметр-Робертсон-Уокер (ФЛРУ) метрикасы, ол біртекті (изотропты) және біркелкі (гомогенді) ғаламның динамикасын сипаттайды, космологияның негізін құрайды және ғаламның кеңеюін сипаттайды.[10]
Гравитациялық толқындар бойынша Эйнштейн өріс теңдеулерінің сызықтық емес шешімдері кеңістік-уақыттың толқынды деформациялары ретінде таралатын гравитациялық толқындардың бар екенін болжайды. Бұл 2015 жылы LIGO тәжірибесі арқылы расталды.
Эйнштейннің өріс теңдеулері :

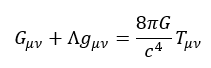
— қазіргі физиканың іргетасын құрайтын ең маңызды жетістіктердің бірі. Олар гравитацияны күш емес, геометриялық құбылыс ретінде ұсынып, қара құрдымдар, ғаламның кеңеюі және гравитациялық толқындар сияқты ғарыштық құбылыстарды сипаттауға мүмкіндік берді. Бұл теңдеулерді одан әрі зерттеу, әсіресе оларды кванттық механикамен біріктіру («Кванттық Гравитация теориясын» жасау) қазіргі теориялық физиканың басты міндеті болып қала береді.[11]
Эйнштейн теңдеулері — қазіргі космологияның, астрофизиканың және кванттық гравитация ізденістерінің негізі. Тензорлық құрылым гравитацияны геометриямен біріктіреді. Эйнштейн теңдеулері Ньютон гравитациясының жалғасы емес, оның тереңдетілген формасы. Егер материя болмаса Tμν=0, кеңістік-уақыт тегіс болады немесе тек гравитациялық толқындар таралуы мүмкін.
Эйнштейн теңдеулері физиканың үш үлкен саласының негізі:[12]
— Космология : Ғаламның кеңеюі, Big Bang, қараңғы энергия;
— Астрофизика:Қара құрдымдар, нейтрон жұлдыздар, гравитациялық линзалар;
— Кванттық гравитация: Уақыт кеңістігінің кванттық табиғатын зерттеу;
Космологиялық Λ-модель — қазіргі стандартты космологиялық модель. Ол Ғаламның динамикасын, кеңеюін және құрылымының қалыптасуын сипаттайды. Модель жалпы салыстырмалылық теориясына және астрономиялық бақылауларға негізделген.
Λ-моделі ғалам біртекті және изотропты деп қарастырылғанда және Фридман–Леметр–Робертсон–Уокер (FLRW) метрикасына сүйенеді, яғни:

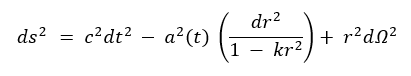
Бұл теңдеуде , a(t) — масштаб коэффициенті, ғаламның уақыт бойынша кеңеюін немесе жиырылуын сипаттайтын функция, a — масштаб коэффициентінің уақыт бойынша туындысы, ғаламның кеңею жылдамдығы, Хаббл параметрі H(t); ғаламның салыстырмалы кеңею жылдамдығы, ρ — ғаламдағы заттың (материяның, энергияның) орташа тығыздығы.
Кеңею динамикасы Фридман теңдеулері арқылы анықталады:

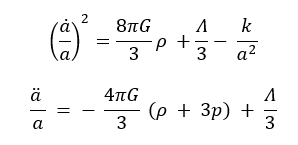
Космологиялық тұрақты Λ — вакуум энергиясының тығыздығы. Ол ғаламның үдемелі кеңеюін тудырады.
Фридман-Леметр-Робертсон-Уокер (ФЛРУ) метрикасын Эйнштейннің өріс теңдеулеріне қойғанда, олар Фридман теңдеулері деп аталатын екі теңдеуге дейін жеңілдейді. Бұл теңдеулер Λ және T_μν (материя тығыздығы) арқылы масштаб коэффициентінің a(t) қалай өзгеретінін, яғни Ғаламның эволюциясын сипаттайды.
Фридман теңдеулері Ғаламның жасын, тығыздығын және болашақ тағдырын есептеу үшін қолданылатын космологияның негізгі құралдары болып табылады.[13]
Ғаламның кеңею динамикасы масштаб коэффициенті a(t) — Фридман-Леметр-Робертсон-Уокер (ФЛРУ) метрикасының (Эйнштейн теңдеулерінің космологиялық шешімі) негізгі функциясы. Бұл коэффициент бізге уақыт өте келе Ғаламның өлшемі қалай өзгеріп жатқанын көрсетеді.
Масштаб коэффициенті a(t) уақыттың (t) белгілі бір сәтіндегі Ғаламның кез келген екі нүктесі (галактикалар немесе галактикалар шоғыры) арасындағы қашықтықты, t₀  (қазіргі уақыт) сәтіндегі олардың қашықтығымен салыстырады және өрнегін мына түрде береміз:[14]

D(t) = a(t)⋅ D₀

Бұл жерде D(t) -t уақытындағы екі объектінің арақашықтығы, D₀ – қазіргі уақыттағы (t₀ ) (немесе бастапқы уақыттағы) олардың координаттық қашықтығы (яғни, кеңеюді алып тастағандағы қашықтық), a(t) – Масштаб Коэффициенті, a(t)-ның уақыт бойынша қалай өзгеретінін білу арқылы біз Ғаламның кеңею жылдамдығын анықтай аламыз. Бұл жылдамдық Хаббл Параметрі (H(t)) арқылы былай сипатталады:

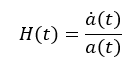
Мұндағы a ̇(t) – масштаб коэффициентінің уақыт бойынша туындысы, яғни оның өзгеру жылдамдығы.[15]
H(t) шамасы Ғаламның белгілі бір уақыттағы салыстырмалы кеңею жылдамдығын береді. t₀ (қазіргі уақыт) сәтіндегі Хаббл параметрі Хаббл Тұрақтысы (H₀ ) деп аталады, бұл Ғаламның қазіргі кеңею жылдамдығын көрсетеді.
Масштаб Коэффициенті a(t) Эйнштейн теңдеулерінің космологиялық шешімдерінің жүрегі болып табылады. Ол арқылы біз ғаламның өткенін (Үлкен жарылыс), қазіргі кеңею жылдамдығын (Хаббл тұрақтысы) және болашақ эволюциясын (Күңгірт энергияның әсері) толық сипаттай аламыз. [15]
Жалпы салыстырмалылық теориясына негізделген қазіргі космологияда Ғаламның кеңеюі уақыт бойынша масштаб факторы a(t) арқылы сипатталады. Масштаб факторы кеңістік өлшемдерінің уақыт бойынша қалай өзгеретінін көрсететін космологиялық функция болып табылады. Егер a(t) өсе бастаса, бұл Ғаламның кеңеюі; ал төмендесе — жиырылуы (коллапс) орын алар еді.
Масштаб факторының динамикасы Эйнштейн теңдеулерінің космологиялық шешімі болып табылатын Фридман теңдеулері арқылы анықталады.
Осы теңдеулер арқылы Ғаламның ашық, жазық немесе жабық болу мүмкіндігі және оның болашақ эволюциясы анықталады. [16]
Космологияда тығыздық параметрі Λ маңызды рөл атқарады.
Масштабтық фактордың өсу графигіне талдауын:
— Λ<1 Ашық Ғалам — шексіз кеңейеді — Λ=1 Жазық Ғалам — тепе-теңдік кеңею — Λ>1 Жабық Ғалам — тоқтап, жиырылуы мүмкін бойынша қарастырамыз.
Берілген графикте ғаламның масштабтық факторы a(t) уақытқа тәуелді қалай өзгеретіндігі көрсетілген. Масштабтық фактор — космологиядағы негізгі функция, ол кеңістіктің жалпы өлшемінің уақыт бойына өзгеруін сипаттайды. Егер a(t) өссе, ғалам кеңейеді; егер кемісе — ғалам жиырылу фазасына түседі. Масштабтық фактордың динамикасы Эйнштейн өріс теңдеулерінен алынатын Фридман теңдеулері арқылы анықталады:

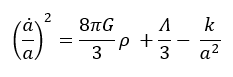
мұнда Λ — космологиялық тұрақты. Осы тұрақтының мәнін өзгерту ғаламның кеңею жылдамдығына тікелей әсер етеді.
Графикте үш түрлі Λ мәндері үшін шкалаланған a(t) функциялары салыстырылған:
1. Λ=0.1 (сары сызық), бұл жағдайда космологиялық тұрақтының мәні өте аз, сондықтан кеңею қарқыны баяу жүреді. Гравитациялық тартылыс басым рөлде болып, ғаламның кеңеюі тежелген күйде көрінеді. [17]
Физикалық интерпретация:
— мұндай ғаламда қараңғы энергияның ықпалы әлсіз;
— кеңею қарқыны уақыт бойынша баяу өседі;
— жазық немесе сәл ашық ғалам сценарийіне жуық.
2.Λ=0.3 (көк сызық), орташа мәндегі космологиялық тұрақты кеңеюді жылдамдатады және ΛCDM моделіне жақын келетін параметр алынады.
Физикалық интерпретация:
— ғалам үдемелі түрде кеңейе бастайды;
— гравитация мен қараңғы энергия арасындағы тепе-теңдік байқалады;
— масштабтық фактор уақыт өтуімен біртіндеп артады.
3. Λ=1.0 (жасыл сызық), үлкен космологиялық тұрақтыға сәйкес келетін модель. Мұнда қараңғы энергия әсері өте күшті.
Нәтижесі: [17]
— кеңею экспоненциалды сипат алады;
— масштабтық фактор уақыттың аз аралығында күрт өседі;
— ғаламның болашағы — шексіз үдемелі кеңею (de Sitter фазасы). Мұндай мысалда Ситтер кеңістігіне жуық, яғни вакуум энергиясы басым ғалам болып есептеледі. Сондықтан масштаб факторының әр түрлі Λ мәндеріне тәуелді графигін салу — Ғаламның эволюциясын модельдеудің негізгі әдістерінің бірі деп есептесек, онда тығыздықтары кез келген жағдайдағы параметрлері үшін масштаб факторының эволюциясын көрсететін диаграмма алуға болады.

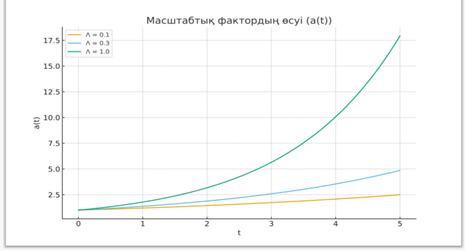
Әр түрлі тығыздық параметрлері үшін масштаб факторының эволюциясы.»»
Бұл график — ғаламның масштаб факторының a(t) уақытқа тәуелді эволюциясын көрсетеді. Үш қисық бар: [18]
— Λ=0.1 — ашық және баяу тығыздықтағы ғалам;
— Λ=0.3 — қазіргі өлшемдерге жақын мән;
— Λ=1.0 — критикалық тығыздықтағы жазық ғалам.
Бұл график Эйнштейн–Фридман теңдеулерінен алынған ғаламның масштаб факторының a(t) уақыт бойынша өзгеруін көрсетеді. Қисықтар әр түрлі тығыздық параметрлері Λ үшін салыстырылған. [18]
Графиктен көрініп тұрғандай, тығыздық азайған сайын кеңею жылдамдығы жоғарылайды, себебі гравитациялық тежелу әлсіз болады. Бұл ΛCDM космологиясымен сәйкес келеді: Ғаламның заттық тығыздығы азайған сайын кеңею қарқыны артады. График Ғаламның динамикасы Эйнштейн теңдеулерімен анықталады. График масштабтық фактордың уақытқа тәуелді эволюциясын көрнекі түрде сипаттайды және Эйнштейн теңдеулері арқылы алынған космологиялық модельдердің физикалық интерпретациясын нақты көрсетеді. Космологиялық тұрақты Λ өскен сайын кеңею қарқыны да арта түсетіні графиктен анық байқалады. Бұл қараңғы энергияның ғалам эволюциясындағы шешуші рөлін дәлелдейтінін көрсетеді. [18]
Қорытынды
Эйнштейннің жалпы салыстырмалылық теориясы қазіргі космологияның негізгі ғылыми әрі математикалық іргетасы болып табылады. Бұл теория гравитацияны классикалық түсініктегідей күш ретінде емес, кеңістік-уақыттың геометриялық қасиеті ретінде сипаттайды. Эйнштейн өріс теңдеулері арқылы материя мен энергияның кеңістік-уақыттың қисықтығын тудыратыны, ал геометриялық құрылымның өз кезегінде материя қозғалысын анықтайтыны дәлелденді. Космологиялық модельдерді сипаттауда масштаб факторы a(t) негізгі рөл атқарады. Ол Ғаламның уақыт бойынша қалай кеңейетінін көрсетіп, оның тарихи эволюциясын және болашақ тағдырын анықтауға мүмкіндік береді. Фридман теңдеулері Эйнштейн теориясының космологиядағы шешімі болып табылады және олар арқылы ғаламның динамикасы тығыздық параметрі Λ мен космологиялық тұрақты Λ арқылы зерттеледі. Масштаб факторының әртүрлі Λ мәндеріне тәуелді графигі ғаламның құрылымы мен эволюциясының мүмкін сценарийлерін айқын көрсетеді. Тығыздық параметрі критикалық мәннен аз болған жағдайда (Λ<1) Ғалам ашық болып шексіз кеңейеді; Λ=1 болғанда — жазық, тұрақты кеңею байқалады; ал Λ>1 болса, ғалам жабық болып, кеңею баяулап, ақырында қайта жиырылуы мүмкін.
Бұл модельдер қазіргі ΛCDM теориясымен үйлеседі және бақылаулармен расталған: Ғалам үдемелі кеңею сатысында, ал вакуум энергиясы немесе космологиялық тұрақты оның басты қозғаушысы болып табылады. Осылайша, Эйнштейн теңдеулері, Фридман космологиясы және масштаб факторының математикалық талдауы ғаламның құрылымы, оның пайда болуы, эволюциясы және болашақ тағдыры туралы терең түсінік береді. Бұл нәтижелер астрофизика мен теориялық физикадағы іргелі мәселелерді шешуге негіз болып, қазіргі ғылыми зерттеулердің маңызды бағытына айналды. Жалпы алғанда, бұл жұмыс Эйнштейн теңдеулерінің құрылымы мен физикалық мазмұнының космологиядағы маңызын ашып көрсетеді. Ғаламның кеңеюін, геометриялық қасиеттерін, энергия тығыздығының әсерін және қараңғы энергия феноменін түсіндіруде Эйнштейн теориясы қазіргі ғылымның негізгі теориялық негізі болып қала береді.

Әдебиеттер

1. https://kaz.inform.kz
2. Эйнштейн А. К теории гравитационных полей // Preussische Akademie der Wissenschaften. — Berlin, 1915.
3. Einstein A. The Foundation of the General Theory of Relativity // Annalen der Physik. — 1916. — Vol. 49.
4. Landau L. D., Lifshitz E. M. Теория поля. — 4-е изд. — М.: Наука, 1988. — 512 с.
5. Weinberg S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. — New York: Wiley, 1972. — 657 p.
6. Misner C., Thorne K., Wheeler J. Gravitation. — San Francisco: W. H. Freeman, 1973. — 1279 p.
7. Mukhanov V. Physical Foundations of Cosmology. — Cambridge University Press, 2005. — 442 p.
8. Peebles P. J. E. Principles of Physical Cosmology. — Princeton University Press, 1993. — 718 p.
9. Hawking S., Ellis G. The Large Scale Structure of Space-Time. — Cambridge: Cambridge University Press, 1973. — 391 p.
10. Carroll S. Spacetime and Geometry: An Introduction to General Relativity. — Addison Wesley, 2004. — 528 p.
11. Reissner H. Über die Eigengravitation des elektrischen Feldes // Annalen der Physik. — 1916.
12. Nordström G. On the Energy of the Gravitational Field in Einstein’s Theory // Proceedings of the Royal Netherlands Academy of Arts and Sciences. — 1918.
13. de Sitter W. On the Relativity of Inertia: Remarks Concerning Einstein’s Latest Hypothesis // Proceedings of the Royal Netherlands Academy. — 1917.
14. Friedmann A. Über die Krümmung des Raumes // Zeitschrift für Physik. — 1922. — Bd. 10.
15. Friedmann A. Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes // Zeitschrift für Physik. — 1924.
16. Planck Collaboration. Cosmological parameters // Astronomy & Astrophysics. — 2020. — Vol. 641, A6.
17. Liddle A. An Introduction to Modern Cosmology. — Wiley, 2015.
18. Riess A. et al. Observational Evidence from Supernovae for an Accelerating Universe // AJ, 1998.